
Interpolation can be effective in data sets that show a clear trend. For example, a statistician might use interpolation to estimate how many people lived in a city in a year between two census administrations which can help them draw conclusions about the city's past. You can also use interpolation to understand historical trends where information is incomplete or missing. Knowing how many products a team might make with a certain number of members might help you decide how many people to have on your manufacturing team. Interpolation can help you make decisions or adjust procedures to maximize productivity. Y = 152 + (170-152) x Īccording to the interpolation formula, a team with 13 members might produce 161 products per day. Using the order of operations, solve for y: Here's how our example points fit into the formula: For x1 and y1, use the input and output from the lower value, and for x2 and y2, use the input and output from the higher value. In the interpolation formula, Y is the desired value, or the output of a team with 13 members. Enter values into the interpolation equation According to the data, a team of 12 has an output of 152, while a team of 14 has an output of 170. For this example, we can estimate the output of a team with 13 members by entering the input and output values for teams of 12 and 14 into the interpolation equation. The interpolation equation can determine a missing value within the boundaries of the data set once you choose the independent variable you want to use. Related: Linear Regression: A Definitive Guide 3. You can also use the graph to confirm that your data set is a good fit for linear interpolation. Creating a graph can help you visualize where your new data point might be in relation to the rest of the data. A line of best fit is a straight line that comes as close as possible to the points in a scatterplot, showing the general trend of the data. You might plot your points onto a coordinate plane using a calculator or graphing program and drawing a line of best fit through your points.
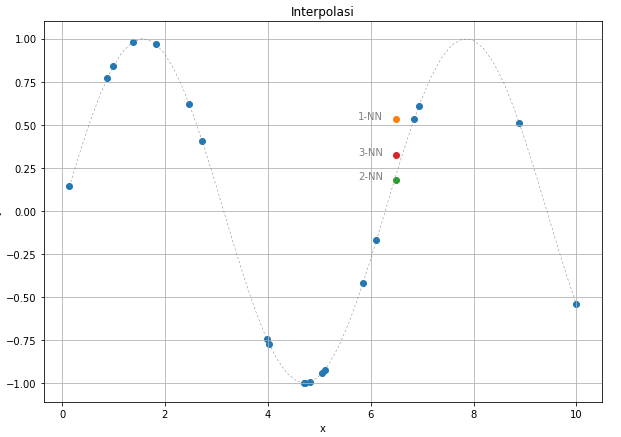
Nonlinear Equations: Understanding the Key Differences 2. You can organize this data in a chart that shows the team size as the independent variables (or x values) and the number of products they create per day as the dependent variables (or y values): Independent variables are the numbers you choose, while dependent variables are the values that correspond to those numbers.įor example, you might measure the productivity of different-sized teams in a manufacturing plant, gathering information on the daily output of teams of 12, 14, 16, and 18. Organize your dataįirst, put the data you've collected into a chart that shows your independent and dependent variables.
#Transtype 4 interpolation how to#
Here's how to use linear interpolation to calculate a value within a data set: 1. For more complicated data sets, you might use a calculator or computer program to perform quadratic or spline interpolation. You can use linear interpolation if your data creates a line when you graph it on a coordinate plane. The simplest form of interpolation is linear interpolation, which can produce an estimated output for an input that falls within the domain of a linear function. The basic equation for linear interpolation is: There are several types of interpolation, including linear, polynomial and spline, which use different equations and may suit data sets with varying distributions. The interpolation formula allows you to find a more precise estimate of an added value. When you're looking at a line graph or function table, you might estimate values that fall between two points or entries. Interpolation is the process of deducing the value between two points in a set of data. In this article, we explain what interpolation is, demonstrate how to interpolate from a set of data and describe how you might use this technique to improve your data analysis. If you use data to measure productivity, efficiency or other metrics in your work, understanding interpolation might help you use your data collection methods more effectively. Collecting and analyzing data can help you improve your work methods and adjust the resources dedicated to a specific process.

Data collection can be a useful tool for many professionals in their careers.


 0 kommentar(er)
0 kommentar(er)
